OLMAR pour OnLine portfolio selection with Moving Average Reversion.

Cet algorithme entend profiter de l’aspect ‘mean reverting‘ des marchés grâce à une technique d’apprentissage (machine learning). Il reçoit en entrée des données, et sur la base de celles-ci, il produira une prévision pour l’incrément suivant. Cette prévision sera utilisée pour construire le portefeuille maximisant le rendement espéré en utilisant un algorithme passif-agressif (Passive Aggressive learning). L’idée de base est de minimiser les écarts de pondération entre le portefeuille actuel et le portefeuille cible qui incorpore les prévisions de rendements.

Prévisions des rendements

Si l’on part du principe que l’ensemble des opérateurs de marchés sont rationnels, alors on peut imaginer qu’ils vont essayer d’exploiter les opportunités d’arbitrage qui s’offrent à eux. Si le prix d’un actif s’écarte fortement à la baisse de sa valeur fondamentale, alors il sera acheté, inversement, s’il s’écarte trop à la hausse, il sera vendu. Ces opérations d’arbitrage vont ramener le prix du titre à sa valeur fondamentale, concrétisant le phénomène de retour à la moyenne. Cette hypothèse (qui a été corroborée par de nombreuses analyses empiriques) implique donc que lorsque ce phénomène se produit, il est possible de fournir une prévision robuste de l’évolution d’un titre, qui est tout simplement basée sur son évolution passée. Ainsi, l’évolution du prix en t+1 devrait être égale à l’inverse de celle en t-1.

Mathématiquement, on a :

Mais les données journalières sont des données très bruitées alors pour filtrer ce bruit on utilise une moyenne mobile sur plusieurs jours.

avec la duration de la moyenne mobile.

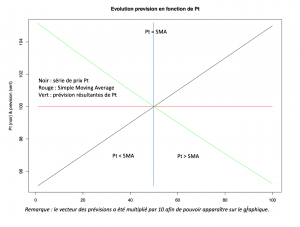
Le schéma ci-dessous nous donne une représentation du fonctionnement de la prévision :

On voit très bien que lorsqu’il y a un écart important entre le dernier prix Pt et la moyenne mobile sur les derniers jours, alors la prévision sera d’autant importante. On remarque également que tant que le dernier prix Pt est supérieur à la moyenne mobile, alors la prévision pour l’incrément suivant est inférieure à 1, et lorsque le prix Pt est inférieur à sa moyenne mobile, la prévision est supérieure à 1, ce qui caractérise bien le phénomène de retour à la moyenne.

Comment fonctionne l’algo ?

L’idée de base est de maximiser la performance en exploitant la prévision des rendements, grâce à l’algorithme passif agressif. A chaque incrément, les poids qui seront en ligne avec les prévisions, bougeront peu, alors que ceux qui en seront éloignés vont significativement changer. Si le marché est mean reverting, alors un écart à la moyenne est une erreur qui sera corrigée par le marché. C’est l’exploitation de cette erreur qui justifie le terme d’agressif, car lors du travail d’optimisation, quand on va tenter de minimiser la distance entre le portefeuille actuel et le portefeuille cible, ce sont les titres dont les prévisions s’écartent le plus de la prévision moyenne qui subiront les réajustements les plus importants. En revanche, ceux dont la prévision est proche de la prévision moyenne, changeront moins. L’idée n’est pas ici de vérifier si dans l’absolu, la prévision est bonne au regard de la valeur elle-même, la prévision est surtout importante par rapport à la prévision moyenne de l’univers.

Si l’on part du principe que le marché est ‘mean reverting’ alors l’équation juste au-dessus fournit une prévision robuste de l’évolution du portefeuille pour la date t+1. En t+1, sa valeur devrait être égale aux poids actuels (vecteur b) drifté des prix en t+1, soit .

Schématiquement, l’erreur est définie comme la différence entre chaque prévision et la prévision moyenne :

avec .

La mise à jour des poids pour l’incrément suivant sera comme suit :

(1)

avec le multiplicateur de Lagrange.

On remarque également, que le seuil de réversion est important car si la solution actuelle (le portefeuille drifté des prévisions) est supérieure au seuil de réversion (lambda vaut zéro), alors il n’est pas nécessaire de changer le portefeuille, mais lorsque ce n’est pas le cas, on change les pondérations.

Le problème revient donc à minimiser les erreurs de pondérations dues aux prévisions lorsque lambda est supérieur à zéro :

Dans l’exemple de cet article, l’interdiction de vente à découvert facilite le programme d’optimisation, et nous permet d’utiliser l’algorithme du simplexe pour obtenir nos pondérations optimales (voir [3]), ce qui permet également de réduire grandement les temps de calculs.

Analyse

On voit bien en regardant l’équation (1) que la mise à jour des poids pour l’incrément suivant, est fonction de deux facteurs (lambda et l’erreur de prévision). Lorsque l’erreur de prévision est faible pour un titre, tend vers 0. Ce faisant, il gardera le même poids qu’avant. En revanche, si l’erreur de prévision est importante, son poids sera revu à la hausse ou à la baisse, en fonction de l’ampleur de l’erreur de prévision et de son signe.

si et si

On l’a vu plus haut, la prévision pour l’incrément suivant est fonction de l’écart du dernier prix par rapport à sa moyenne mobile sur plusieurs jours. Ainsi, lorsque le dernier prix s’écarte fortement de sa moyenne mobile, à la hausse ou à la baisse, il marque une certaine rupture dans sa tendance, et plus il s’écartera du marché, plus une opportunité va se concrétiser.

Définition des backtests

La méthodologie du backtest suit celle qui est mentionnée dans l’article que je cite [1]. On considère un investissement dans m actifs durant n périodes. On valorise la stratégie avec les cours de clôtures qu’on exprime de façon vectorielle avec et où chaque élément du vecteur représente le cours de clôture de l’actif i. La variation du prix est représentée par un vecteur de prix relatif , avec . Un investissement à une période t est représenté par un vecteur de portefeuille , où représente la proportion du portefeuille investit dans l’actif i. En faisant l’hypothèse que notre stratégie est financée et que les positions short sont interdites, aucun élément de notre vecteur ne peut être négatif et la somme des poids doit être inférieure ou égale à 1.

A l’instant t, le portefeuille produit un rendement sur la période égale à .

Comme on utilise les prix relatifs pour valoriser la stratégie, la valeur du portefeuille va croître de façon multiplicative. Après n périodes, le portefeuille va produire une valeur cumulée égale à , qui viendra augmenter (ou baisser) la valeur initiale du portefeuille par un facteur de , qu’on peut également écrire comme où est l’investissement initial.

Dans tous les backtests, la stratégie OLMAR est comparée à une stratégie ‘Equal Weighted‘.

Mes données

Dans un premier temps, j’ai essayé de reproduire les résultats de l’auteur en utilisant ses données (on peut les trouver ici). Elles concernent exclusivement les marchés actions américains, c’est pourquoi j’ai également décidé de tester la stratégie sur des actions européennes. Bien que j’ai essayé d’éviter tout biais dans mes backtests, il en existe toujours un peu, et notamment le biais du survivant, puisque je n’utilise que des valeurs encore existantes. Dans les données de l’auteur, dont je publie un backtest juste en dessous, il existe également un biais ‘look ahead bias’, car les données qui sont backtestées entre 1998 et 2003, sont constituées des plus grosses capitalisations de l’indice en 2003. C’est comme si dès 1998, nous connaissions les valeurs qui progresseraient le mieux jusqu’en 2003 (au regard du lien qui peut exister entre la capitalisation et la performance boursière d’un titre). Malgré tout, dans tous mes backtests, je compare la performance de la stratégie à celle d’un portefeuille équipondéré (sachant qu’il a été démontré dans la littérature financière, que l’équipondération est une stratégie qui donne souvent de meilleurs résultats que les indices de capitalisations), donc le biais existe pour les deux stratégies.

Quelques backtests

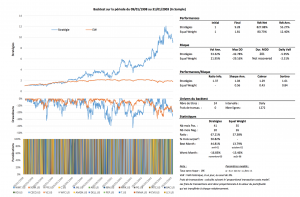
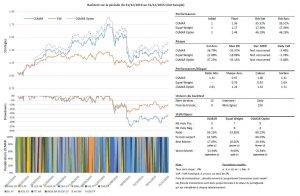
Sur un des univers de l’auteur :

Le backtest au-dessus, reprend l’univers S&P 500 définit par l’auteur (dont le lien est plus haut). Étant donné que je n’ai pas été capable de récupérer les données du titre SBC Communication, je l’ai retiré de l’univers. Le fait de retirer cette valeur, diminue significativement les résultats, mais ils restent intéressants. Pour ce backtest, j’ai utilisé les paramètres conseillés par l’auteur, qui sont w = 5 et e = 10.

Le tableau ci-dessous rend compte de la sensibilité des performances au choix des paramètres w et e :

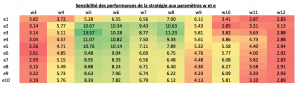
Remarque : ici les backtests commencent en date du 30/01/1998. Le tableau reprend la valorisation finale de la stratégie à la dernière date du backtest, sachant qu’on commence avec 1$ (ou €) d’investissement. Rappel : les frais de transactions sont nuls.

Sur un univers d’actions européennes :

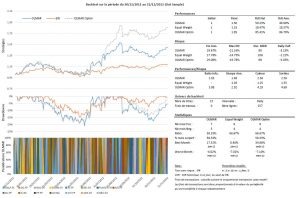
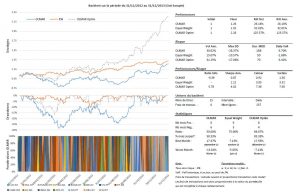
Dans un premier temps, j’ai construit un univers des 30 plus grosses capitalisations françaises et allemandes, en date du 31/12/2010. J’ai effectué des backtests sur deux périodes afin de savoir s’il était possible d’extraire les paramètres optimaux pour la période ‘out-sample’. La période ‘in-sample’ court du 30/12/2005 au 31/12/2010, la période ‘out-sample’, du 31/12/2010 au 31/12/2015.

Résultats des simulations sur l’univers français : Backtests_univers_France

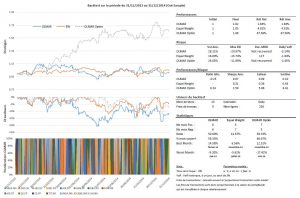
Résultats des simulations sur l’univers allemand : Backtests_univers_Allemagne

Il ressort des résultats que les paramètres optimaux ne semblent pas stables à travers le temps, et qu’une méthode aussi naïve ne fonctionne pas. Si j’utilise les paramètres qui ont le mieux fonctionné entre le 2006 et 2010 pour la stratégie en période ‘out-sample’, j’obtiens des résultats médiocres. Sur l’univers français, en période ‘in-sample’, les paramètres optimaux correspondaient à la combinaison w = 21 et e = 12, tandis que sur la période ‘out-sample’, ils correspondaient à w = 19 et e = 4. La réutilisation des paramètres de la période in-sample sur la période out-sample conduit à obtenir une performance de +154% alors qu’avec les paramètres optimaux j’aurais eu une performance de +275%. Même rengaine sur les autres univers !

Ces résultats montrent également que le choix de l’univers est important. En effet, contrairement aux résultats sur les univers français et américains, les résultats sur l’univers allemand sont pitoyables. Sur l’univers français, on voit que la stratégie offre une meilleure performance (et je parle ici uniquement de performance, car cette statistique serait bien différente si l’on regardait le ratio de Sharpe) que la stratégie ‘Equal Weighted’ dans plus de 82% des cas (out-sample), tandis que sur l’univers allemand, la stratégie OLMAR n’arrive pas à battre la stratégie ‘Equal Weighted’ une seule fois.

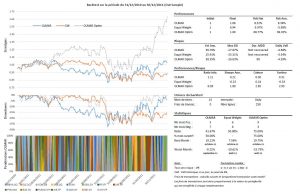
Dans les backtests ci-dessous, j’essaie d’améliorer le choix de l’univers. Chaque fin d’année, entre 2010 et 2014, je crée un nouvel univers composé des 15 sociétés possédants le meilleur alpha estimé contre l’Eurostoxx 50 dividendes nets réinvestis sur 5 années, sur un univers global composé des 100 plus grosses capitalisations européennes cotant en euro, au 31 décembre 2010. L’univers ainsi définit sera utilisé pour la stratégie de l’année qui suit.

Univers global : Univers LC 100 dec 2010

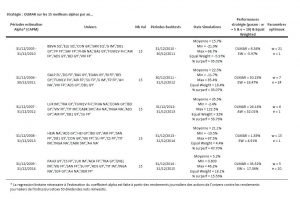
Le tableau ci-dessous reprend les périodes d’estimation pour l’alpha et les univers résiduels ainsi que les résultats des simulations lorsqu’on ne fixe pas, à priori de paramètres et enfin les résultats de la stratégie OLMAR en choisissant arbitrairement les paramètres suivants : w = 5 et e = 10, comme dans l’exemple de l’auteur.

On remarque qu’il existe dans toutes les situations des paramètres optimaux permettant de capter de façon très efficace les phénomènes de retour à la moyenne. Malheureusement, il n’existe pas encore, à ma connaissance, de méthodes pour prévoir les paramètres qu’il faudra utiliser pour les futurs investissements. Cependant, l’utilisation d’univers pertinents permettant d’améliorer significativement les performances, il est possible de fixer arbitrairement des paramètres, comme je l’ai fait dans les backtests. Dans ce cas, je dirais qu’il faut user de parcimonie, car les résultats des simulations montrent que les paramètres optimaux sont rarement extrêmes.

Conclusion

L’étude des simulations numériques donne des résultats quasi similaires à ceux des auteurs du papier : les performances sont globalement bonnes puisque la stratégie enregistre de manière régulière, et sur plusieurs échantillons, des performances meilleures que la stratégie ‘Equal Weighted’. La stratégie souffre cependant de certains déficits. Les portefeuilles générés sont ultra concentrés, se faisant, les bénéfices de la diversification sont inexistants. Le deuxième déficit de cette stratégie est inhérent à beaucoup de stratégies systématiques. En utilisant uniquement des prix en input, on se passe d’informations qualitatives sur les valeurs qui vont être sélectionnées par le modèle. Ainsi, une forte baisse d’un titre, peut-être légitime (faillite, profit warning, détection de fraude, etc) et jouer un retour à la moyenne peut alors être très risqué. L’inverse est également vrai, si le titre progresse fortement. Le vendre en jouant un retour à la moyenne peut conduire à se séparer du titre trop tôt.

Il est cependant intéressant de voir que l’algorithme laisse énormément de place aux améliorations, que ce soit sur la prévision des cours ou sur l’optimisation de portefeuille, ainsi que les univers à utiliser. On a également vu qu’il existe toujours des paramètres optimaux permettant d’améliorer significativement les performances de la stratégie, il serait donc intéressant de créer une méthode permettant d’estimer ces paramètres pour les futurs investissements.

La méthodologie employée pour ces backtests n’est pas sans biais, bien que j’ai essayé d’en éviter le plus possible. Cet article ne constitue en aucun cas un conseil en investissement. Il ne correspond qu’à un point de vue parmi tant d’autres. Malgré tous mes efforts pour éviter les erreurs, je ne saurais assurer qu’il n’y en a pas.

Mes scripts R :

Vous trouverez juste en dessous les scripts que j’ai réalisés pour mes analyses. Ils sont sûrement perfectibles !
En plus du simplex, j’ajoute une fonction qui utilise le package Rsolnp pour effectuer le travail d’optimisation. L’intérêt de passer par ce package est de pouvoir rajouter des contraintes (sur les poids max des lignes du portefeuille par exemple) dans le solveur. Il est par contre beaucoup moins rapide que l’algorithme du simplex.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

### Fonction : algo_OLMAR_simplex ###
# source : On-Line Portfolio Selection with Moving Average Reversion
# Auteurs : Bin Li, Steven C. H. Hoi
# Lien internet : http://arxiv.org/ftp/arxiv/papers/1206/1206.4626.pdf
 
# Variables de la fonction :
# e : seuil de reversion
# b : vecteur des poids du portefeuille avant optimisation
# vec_rel_px : vecteur des prix relatifs
 
algo_OLMAR_simplex <- function(e, b, vec_rel_px){
 
  m <- ncol(vec_rel_px)
  b_new <- matrix(rep(0,m), ncol=m, nrow=1)
 
  x_bar <- matrix(rep(vec_rel_px%*%matrix(rep(1,m), nrow=m)/m, m), ncol=m)
  mar_rel_dev <- as.vector(vec_rel_px-x_bar)%*%as.vector(vec_rel_px-x_bar)
 
  # Lambda
  lambda <- pmax(0, (e-b*vec_rel_px)/rep(mar_rel_dev,m))
 
  b_new <- as.vector(b + lambda*(vec_rel_px-x_bar))
 
  b_new <- fn_Simplex_Optim(b_new, 1)
 
  return(b_new)
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

### Fonction : fn_Simplex_Optim ###
# source : Efficient Projections onto the l1-Ball for Learning in High Dimension
# Auteurs : John Duchi, Shai Shalev-Shwartz
# Lien internet : http://ttic.uchicago.edu/~shai/papers/DuchiShSi08.pdf
 
# Variables de la fonction :
# v : les poids du portefeuille avant optimisation
# z : contrainte de poids maximum (z > 0)
 
fn_Simplex_Optim <- function(v, z){
 
  nr <- length(v)
  rho_vec <- rep(0, nr)
  rho_seq <- seq(1, nr, 1)
  new_w <- rep(0, nr)
  rang <- 0
 
  # Ordonner data en decroissant
  idx <- order(v, decreasing=TRUE)
  u <- v[idx]   # Stockage dans u
  # on doit avoir u1>u2>...>up
 
  # Ici on cherche le rang maximum pour les valeurs de rho > 0
  rho_vec <- as.matrix(u-(cumsum(u)-z)/rho_seq)
  rho_vec[which(rho_vec<0),]<-0
 
  rho_rang <- max(which(rho_vec>0))  
  theta <- (sum(u[1:rho_rang])-z)/rho_rang  
  new_w[idx[1:nr]] <- pmax(0,v[idx[1:nr]] - theta)
 
  return(new_w)
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

### Fonction : algo_OLMAR_solnp ###
# source : On-Line Portfolio Selection with Moving Average Reversion
# Auteurs : Bin Li, Steven C. H. Hoi
# Lien internet : http://arxiv.org/ftp/arxiv/papers/1206/1206.4626.pdf
 
# Variables de la fonction :
# e : seuil de reversion
# b : vecteur des poids du portefeuille avant optimisation
# vec_rel_px : vecteur des prix relatifs
 
algo_OLMAR_solnp <- function(e, b, vec_rel_px){
 
library(Rsolnp)
 
  m <- ncol(vec_rel_px)
  b_new <- matrix(rep(0,m), ncol=m, nrow=1)
 
  x_bar <- matrix(rep(vec_rel_px%*%matrix(rep(1,m), nrow=m)/m, m), ncol=m)
  mar_rel_dev <- norm(as.vector(vec_rel_px-x_bar), type="2")*norm(as.vector(vec_rel_px-x_bar), type="2")
 
  # Lambda
  lambda <- pmax(0, (e-b*vec_rel_px)/mar_rel_dev)
 
  b_new <- as.vector(b + lambda*(vec_rel_px-x_bar))
  assign("b_new", b_new, envir=globalenv())
 
  # Fonction a minimiser
  algo <- function(x){
    return(norm(x-b_new, type="2")*norm(x-b_new, type="2"))
  }
 
  b_new <- solnp(pars=rep(1/m, m), fun=algo, eqfun=sum, eqB=1, LB=rep(0,m), UB=rep(1,m))$pars
 
  return(b_new)
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

### Fonction : fn_Simple_Moving_Average ###
 
# Variables de la fonction :
# data : series de prix
# w : duration de la moyenne mobile (en nombre de jours)
 
fn_Simple_Moving_Average <- function(data, w){
 
  m <- ncol(data) 
 
  x_t <- as.matrix(data)
 
  x_sim <- matrix(rep(0, m), ncol=m, nrow=1)
  x_tmp <- matrix(rep(0, m), ncol=m, nrow=1)
 
  for(i in nrow(x_t):(nrow(x_t)-w+1)){
    x_tmp <- x_tmp + x_t[i,]/w
  }
 
  x_sim <- matrix(x_tmp/x_t[nrow(x_t),], nrow=1)
 
  return(x_sim)  
}

Remarque :

La fonction ci-dessous est celle que j’appelle pour conduire mes backtests. Les données qu’elle reçoit sont des prix (et non des prix relatifs). Si vous souhaitez tester les scripts sur les données de l’auteur (qui sont publiées en prix relatifs), il faudra effectuer quelques modifications. Pour des raisons de place je ne publie pas le code modifié, mais je peux très bien le fournir en cas de besoin.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

### Fonction : fn_OLMAR_Complet ###
# source : On-Line Portfolio Selection with Moving Average Reversion
# Auteurs : Bin Li, Steven C. H. Hoi
# Lien internet : http://arxiv.org/ftp/arxiv/papers/1206/1206.4626.pdf
 
# Variables de la fonction :
# data : serie de prix
# w : duration de la moyenne mobile (en nombre de jours)
# e : seuil de reversion
# inv : investissement de depart
# fees : frais de transaction
# start.date : date depart backtest
# end.date : date fin backtest
 
fn_OLMAR_Complet < -function(data, w, e, inv, fees, start.date, end.date){
 
  data<-as.matrix(data[(which(rownames(data)==start.date)-(w-1)):which(rownames(data)==end.date),])
 
  # Definition des variables pour backtest
  m <- ncol(data) # Nombre de titres dans mon univers (ou mon portefeuille)
  nr <- nrow(data)   # Nombre de jours dans la serie
  w <- w
  e <- e 
 
  w_mat <- matrix(rep(0, m), ncol=m, nrow=nr+1) 
  w_mat[1:w,] <- 1/m
 
  strat <- matrix(rep(0, nr), ncol=1, nrow=nr)
  strat_ew <- matrix(rep(0, nr), ncol=1, nrow=nr)
 
  strat[1:w,1] <- inv
  strat_ew[1:w,1] <- inv
 
  nb_titres <- matrix(rep(0, nr), ncol=1, nrow=nr)
  sub_data_univ <- matrix(rep(0, m), ncol=m, nrow=1)
  px_rebal <- matrix(rep(0, m), ncol=m, nrow=1)
 
  f_ew <- 0
  f_olmar <- 0
  tc <- fees
 
  vec_w_rebal <- matrix(rep(1/m, m), m, nrow=1)
  vec_w_ew <- matrix(rep(1/m, m), ncol=m, nrow=1)
 
  univ <- 0
  b <- matrix(rep(1/m), ncol=m, nrow=1)
 
 
  for(i in w:nr){
 
    univ <- data[,1:m]
 
    delta_w <- abs((w_mat[i-1,]*univ[i-1,]/univ[i-2,])-(w_mat[i,]*univ[i,]/univ[i-1,])) 
 
    delta_w_ew <- abs((vec_w_ew*univ[i-1,]/univ[i-2,])-(vec_w_ew*univ[i,]/univ[i-1,]))
 
    f_olmar <- sum(delta_w)*tc
 
    f_ew <- sum(delta_w_ew)*tc
 
 
    sub_data_univ <- univ[(i-(w)+1):i,]
 
    vec_rel_px <- fn_Simple_Moving_Average(as.matrix(sub_data_univ), w)
 
    w_mat[i+1,] <- algo_OLMAR_solnp(e, w_mat[i,]*(univ[i,]/univ[i-1,]), vec_rel_px) 
 
    rel_px <- as.numeric(univ[i,]/univ[i-1,])
 
    nb_titres[i,] <- length(which(w_mat[i,]>0.005))
 
    # Valorisation des strategies
    strat[i] <- ifelse(i == w, inv, as.numeric(strat[i-1,])*(sum(w_mat[i,]*(rel_px)))-f_olmar)
 
    strat_ew[i] <- ifelse(i == w, inv, as.numeric(strat_ew[i-1,])*sum(vec_w_ew*rel_px)-f_ew)
 
  } 
 
  all_strat <- cbind(strat, strat_ew, nb_titres, w_mat[1:nr,])
 
  rownames(all_strat) <- rownames(data)
 
  all_strat <- all_strat[w:nrow(all_strat),]
 
  col_names_strat <- rbind("OLMAR", "EW", "Nb_lines", as.matrix(colnames(data)))
 
  colnames(all_strat) <- col_names_strat
 
  return(all_strat)
}

Références :

[1] Bin Li, Steven C. H. Hoi. On-Line Portfolio Selection with Moving Average Reversion. HoiThe 29th International Conference on Machine Learning (ICML2012) Edinburgh, Scotland June 26 – July 1, 2012.

[2] Bin Li, Steven C. H. Online Portfolio Selection: Principles and Algorithms. HoiCRC Press November 5, 2015 (212 Pages, ISBN 9781482249637).

[3] John Duchi, Shai Shalev-Shwartz, Yoram Singer, Tushar Chandra. Efficient Projections onto the l1-Ball for Learning in High Dimensions. Appearing on Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 2008.